You are not alone... its nothing like as easy as it looks.
Lots of TBDs, but may be of some use to someone. John 2015-01-02
The pentatonic scale has many variants and a long history. There are lots of web sites, books, and learned papers that document its use across time and cultures. Here I just want to try to show the essence of what makes the pentatonic scale, as it is generally defined and used in most western music, so important. The pentatonic scale we tend to learn first is the minor pentatonic. The pentatonic minor scale is just the 1st, 3rd, 4th, 5th and 7th of the minor scale. There are five patterns (aka positions) for this pentatonic scales. Like any other minor scale, it can be played over the minor chord and its relative major chord. As a result, each of the five pentatonic scale patterns is associated with a minor and a major chord shape, which are the CAGED chord shapes.
This shows the five pentatonic patterns and their associated CAGED minor chords. As well as remembering the association between the pentatonic pattern and the chord shape, it is useful to remember the root note for each of the chords.
This shows the same five pentatonic patterns and their associated CAGED major chords. Note that the relative major of G minor is A#. It is always easy to find the relative major of a minor as it is will be 3 semitones (frets) higher. (Step back one fret and your at the Major 7th, then two frets and its the 6th).
One of the key ingredients of the blues sound is the pushing of a major key into a minor key or visa versa. You can do this in lots of ways. One very useful way is to merge/mash together the major and minor pentatonic scales. So taking Gmajor and Gmin we can merge these to get a scale that has an interesting sound that includes a nice 4 note chromatic run. A second 4 note run can be created by adding in the so called 'blues note'... a flat 5. To create the scale you just take a major pentatonic pattern and merge it with the preceeding pentatonic pattern.
This shows the five pentatonic maj-min patterns:
To understand this section you need to know a bit about 'modes'. This bit is here as it completes the circle of how CAGED chords, pentatonics and modes are all related. I have never seen this made sufficiently clear in any book or web site that I have come across. I suppose to some it may be obvious... it certainly wasn't to me!
There are seven modes, one for each note of the Major scale. However, the scale patterns for the Phygian and Lydian are the same, apart from one note. The same is true of the Ionian and the Locrian. So we only really have 5 distinct scale patterns which are just extensions of the 5 pentatonic patterns. Yes, the penatonic patterns are really the pentatonic notes selected from the modal pattern ... but we are looking at this from the point of view of pentatonics and the CAGED chords.
So the following illustrates the mapping between modal scale patterns and the pentatonic scale patterns. So 'P1' is Minor Pentatonic position one, etc. The blue notes are the penatonic pattern. This example is based on the scale of C Major but obviously it is a moveable feast:
There are five basic Major chord shapes, from which many other chords can be derived. It sometimes requires a strech of imagination as well as fingers, but it is a useful system as it crops up everywhere. There is no deep reason or theory behind this. It is just an artifact of the tuning of the strings and the limitations of the human hand. It may be obvious but do remember that the shape name is not the chord name. The fretboard below shows these chord shapes as variants of the C Major chord. Press the buttons to see the chords. Note how one flows from the other and allows this Major chord to be played in 5 diffent positions up the fretboard.
A major chord contains the root, a Major 3rd and a Perfect 5th. Each of these notes can be duplicated. A minor chord is the same except it has a Minor 3rd, which is just a flattened 3rd. So, in the C Major chords above, the Major 3rd is E, so to create the minor we just need to replace this with Eb. And we get the following basic shapes.
An octave contains 12 unique notes a semitone apart (13 including the octave).
The Major (diatonic) scale consists of the eight notes (including the octave) separated by the intervals: Tone Tone Semitone Tone Tone Tone Semitone [TTS T TTS]. The fifth note in the scale is therefore 7 semitones above the root.
If we start at on the root note of a scale and step up 7 semitones we are on the 5th of that scale. If we then regard this as a new starting point and take another step up of 7 semitones we are on the 5th of this scale. By repeating this exercise 12 times we will visit each of the 12 notes in our original scale.
The reason is simply that 12 does not divide by 7. The remainder of 12/7 is 5 (12 % 7 = 5). So each time we step we are offset by 7 - 5 = 2 semitones. (Until the offset is divisible by 7, so really its: 2n % 7). Step 12 times and you will have visited every note and will be back at the beginning.
Hopefully, the table below illustrates the point.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
The Circle of 5ths is just another way of writing this down. The reason the Circle of 5ths is so important is because of the properties that flow from presenting it in this way.
A final crucial point to notice is that if we step backwards from our starting point to the 5th our step will cover 5 semitones, not 7 ... because 12 - 7 = 5. Five semitones is a 4th, which is why the Circle of 5ths is often also called the Circle of 4ths. In the opposite direction the same arguments apply, its just that in this case 12 is not divisible by 5.
Find the Key
Penatonic Scales
Chord Progressions
Tetra Chords
TBDAn Arpeggio is the 1st 3rd 5th and 7th note of a scale. These are the chordal notes... used to build chords. The 2nd 4th and 6th are not in general used to build a basic chord and are regarded as colour tone notes. They are added to the basic chord to bring extra interest.
So the following are some useful arpeggios:
TBD
The modal scales are built from the major scale and contain the same notes as this parent scale. Each mode starts on a different note in the parent scale. It is very important to remember that the modal scales built from any particular major scale will contain the same notes as its parent. In the table below the Major scale, also known as the Ionian, is at the top and shows the usual Major scale interval pattern of: Tone, Tone, Semitone (between 3rd and 4th), Tone, Tone, Tone, Semitone (between 7th and 1st). [TTSTTTS]
Then each of the modes start on the following notes in the Major scale on the left (the numbers are the note of the parent Major scale). The coloured notes are the notes that are displaced relative to the Major scale pattern [TTSTTTS]. These are the notes that give the particular mode its character. They are sometimes called the character notes. Knowing these and how to use them is one of the most important aspect of using modes.
| 1 | 2b | 2 | 3b | 3 | 4 | 5b | 5 | 5# | 6 | 7b | 7 | 1 | |
| Ionian | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 1 | |||||
| Dorian | 2 | 3 | 4 | 5 | 6 | 7 | 1 | 2 | |||||
| Phrygian | 3 | 4 | 5 | 6 | 7 | 1 | 2 | 3 | |||||
| Lydian | 4 | 5 | 6 | 7 | 1 | 2 | 3 | 4 | |||||
| Mixolydian | 5 | 6 | 7 | 1 | 2 | 3 | 4 | 5 | |||||
| Aeolian | 6 | 7 | 1 | 2 | 3 | 4 | 5 | 6 | |||||
| Locrian | 7 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| the character notes for each mode | ||
| Mode | In Key | In Parent |
| Ionian | none | |
| Dorian | 3b 7b | 4 1 |
| Phrygian | 2b 3b 5# 7b | 4 5 1 2 |
| Lydian | 5b | 7 |
| Mixolydian | 7b | 4 |
| Aeolian | 3b 5# 7b | 1 4 5 |
| Locrian | 2b 3b 5b 5# 7b | 1 2 4 5 6 |
However, bear in mind that each pattern is only named after a mode because the root for that mode is on the 6th string. It is a very confusing convention. It would be better if, like with penatonic scales, we talked in terms of the 1st, 2nd, etc positions (imho!). In reality, any of the modal scales can be played in any of the five positions. You just need to be aware of where the root and the character notes are for a given mode in that position. When playing in a mode these notes need to be emphasised to reveal the modal sound.
So are the modal scale patterns useful? Well yes, because together they cover the whole fret board in a given Major key. The trick is to know the relative Major of the key you want to play in! So an easy example would be; you want to play in A minor, so you can play any modal pattern of C Major. Then to get the 'minor' sound you need to emphasis the 1st 4th and 5th of the relative Major scale. This is equivalent to playing A minor.
A more complicated example would be you want to play get a Phrygian sound over an Emin7 chord. Then you will need to play E Phrygian whose relative Major is again C. So you can play any modal pattern in C and emphasis the character notes the 1st and 4th. You will notice that the character notes are very similar to the previous example. The difference is they are being played against an Emin7 and it is this that gives the modal tonality... but you need to pick out the character notes for it to work effectively.
The position of the character notes within the scale patterns is more easily seen if we label the notes using the parent major scale's note number. If you know where the root note is then it is easy to find the character notes. The diagram below highlights the 1st 4th and 7th as these are the most common character notes. But, of course, the Aeolian mode has the 5th and the Locrian also has the 2nd and 6th. Notice that the 3rd is never a character note. This then can be considered to be the character note of the Ionian, the parent scale.
If you build a chord consisting of the root, 3rd and 5th from each of the modal scales you get 7 chords (usually labelled I II II IV V VI VII) some are major and some are minor because the 3rd is a flattened 3rd relative to the Major scale. So we have:
| Modal Triads | ||
| Ionian | I | Major |
| Dorian | II | Minor |
| Phrygian | III | Minor |
| Lydian | IV | Major |
| Mixolydian | V | Major |
| Aeolian | VI | Minor |
| Locrian | VII | Half Diminished |
One of the many things to notice is how the the common blues progression I IV V is all the major triads.
TBD
A diatonic scale is 8 notes distributed over 12 semitones. There are many combinations for this:
Most of these combinations make no musical sense. So what makes a scale work? One rule is it must consists of 5 tone intervals and 2 semitone intervals. But what determines the distribution and is it necessary to impose any rules for this structure to emerge?
I think the answer may be that the notes attempt to distribute evenly but 12 does not divide by 7 which leads to the structure of scales and other artefacts like the circle of fifths. There is no need to impose the rule; 5 tones and 2 semitones, this emerges as having the most stable structure.
Imagine a string of eight beads on a wire of fixed and finite length. If each bead repels the other beads according to some law r = R(d) where d is the distance from the centre of a bead to another bead then the beads will arrange themselves with equal spacing between them. The form of the law is immaterial as long as it decays monotonically with distance. The equal spacing will represent the point of lowest energy for the system.
So, if we assume the wire is of length 12, then the energy function will be of the form:
where
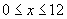then the energy is at a minimum at 0, q, 2q, 3q, 4q, 5q, 6q, 7q where
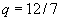representing the 8 notes of a diatonic scale.
If however, the positions on the wire do not have equal potential energy, like for instance a wire that attracts the beads to particular positions, then it is the interplay of these two potential energy fields that will determine the position of the beads.
If we model the position of the notes in a diatonic scale this way we can show that the scales that emerge are the same as those that we use and they exist because they form a stable system.
So there are 12 notes in an octave, representing 11 intervals of 1 semitone (the details of Equal Temperament versus Just Intonation and other tunings do not change this assumption).
There are 8 notes in a standard scale and 7 intervals. We are excluding pentatonic, chromatic, and other exotica as these are all derived scales but the same principals still apply.
If we provide a field along the wire that provides the energy minima at the 12 points of the scale then how will the scale notes distribute themselves to minimise the system's overall energy?
Assume the energy distribution along the wire is:
where 
then the energy is at a minimum at 0,1,2,3,4,5,6,7,8,9,10,11,(12) representing the 12 semitones of a diatonic scale.
If we combine these two energy functions and provide some relative weighting then we get:
With w = 1 then the graph looks like:
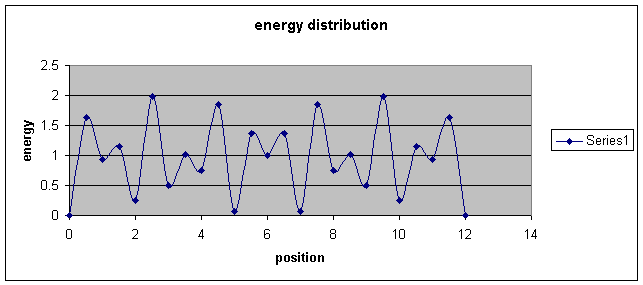
From the graph one can see that the most stable (with least energy) notes are at: 0,2,5,7,10 and 12
In scale of C Major we have:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7b |
7 |
8 |
||||
|
C |
D |
E |
F |
G |
A |
Bb |
B |
C |
So these are the tonic, the 2nd, the perfect 4th, the perfect 5th, the flattened 7th and the octave.
The others notes can take up a variety of positions but are less stable.
Also, the scale is symmetric about position 6 (flattened 5th) which is true of just the Ionian, Dorian and Phrygian scales, that is the first three modal scales. If T=tone and S=semitone the Ionian major scale is TTS T TTS and the Aeolian minor is TST T STT.
If we take the 8 most stable notes from the graph we have TST T TST, which is the Dorian scale.
The other modal scales therefore all have slightly higher overall energy, which is an interesting result. The Dorian scale is the first of the modal minor scales and is symmetric and does have a particularly pleasing sound.
So maybe the lower a scale's energy (ie stability) the more mellow. The higher the energy the more challenging. On this basis you can order the modal scales by relative stability:
| Stability | Scale | Intervals |
| 1 | Dorian | TST T TST |
| 2 | Aeolian | TST T STT |
| 2 | Mixolydian | TTS T TST |
| 3 | Ionian | TTS T TTS |
| 4 | Phrygian | STT T STT |
| 5 | Lydian | TTT S TTS |
| 5 | Locrian | STT S TTT |
If you play each of these scales in this order there does appear to be an increasing sense of tension? Interestingly, the Ionian sits in the middle of the range of stability, not at the top. From there you can head towards the mellow Dorian or to the jazzy Locrian ?
Also, another observation is that when resolving to the octave the sound that often provides the biggest sense of resolution is the resolution of 7th to the octave or the flattened 2nd to the tonic. From the graph, both require the biggest energy change between two adjacent semitones.
It all sort of seems to work and to reflect reality...a bit ?!
12 * n is not divisible by 7 where n < 7
A fifth is 7 semitones. A fourth is 5 semitones.
So: 4th + 5th = octave
So to pass through all the notes in steps of 7 semitones you need to iterate over the octave of 12 semitones 6 times picking the 2 notes (x and y) 7 or 5 semitones apart x --> y = 7 or y --> x = 5
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| C | D | E | F | G | A | B | C | ||||||
| 1 | x | y | |||||||||||
| 2 | x | y | |||||||||||
| 3 | x | y | |||||||||||
| 4 | y | x | |||||||||||
| 5 | y | x | |||||||||||
| 6 | y | x |
The Circle of 5ths is just an artefact of 12 not being divisible by 7.
There are hundreds of guitar sites out there. Some good ones and some 'not so good'. This is just a few sites for getting tab that google often doesn't reveal in the first few pages:
http://acousticpower.com A site with 100's of free PowerTab files
http://www.freetabs.org/listtabs.htm Lots of tabs ... mostly tef files.
http://www.acousticfingerstyle.com/midifils.htm Some interesting tab from a variety of artists
http://www.hotclub.co.uk/ptab/powertab.html Lots of jazz tunes in powertab format
http://www.willflyguitar.com/tablatures.html Tab arrangements by Will Fly
http://justinguitar.com Of the instructional sites I think this is one of the best.
http://www.tallstrom.com Martin Tallstrom ... many playing styles
http://www.boegershausen.de Ulli Bögershausen ... fine player and free tabs
Scales are the foundations of music. It is a huge subject and there are many many different types of scale. But here we are just concerned with the basic definition of the kind of scales used in most popular western music.
An octave contains 13 notes each separated by a semitone... so 12 distinct notes. The Major Scale is defined as the 8 notes (including the octave) over these 12 notes such that they are separated by intervals of a tone or a semitone as follows: Tone Tone Semitone Tone Tone Tone Semitone (ie TTSTTTS). So for C Major we have C D EF G A BC. This is an example of a diatonic as it obeys the general rule that a diatonic scale must have five tone intervals and two semitone intervals that are separated. So that the Major Scale is a specific example of this rule. It is of no real significance for us at the moment but the word 'diatonic' is often thrown into descriptions, so it is good to be vaguely aware of what it means!
The Major scale is the basis of the other common scales. By changing some of the intervals we can arrive at the Minor scale and many other exotica.
TBD
(need to move this) The formula for the frequencies of the notes of the Equal Tempered scale is just: fn = f0 * (a)n where
